Les transformations:

I. Rappels : symétries, translations, rotations:

1. Symétrie axiale:

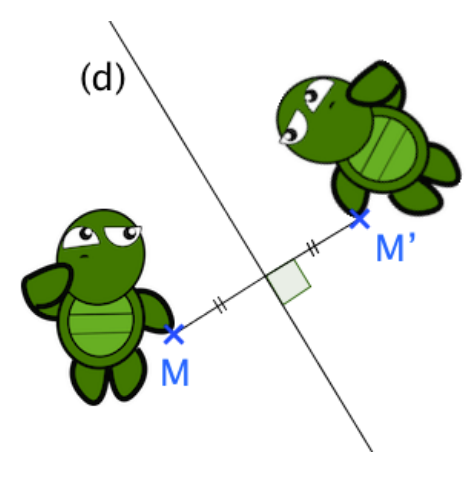
Deux points M et M' sont symétriques par rapport à une droite (d) si : - [MM'] est perpendiculaire à (d)

- la droite (d) coupe le segment [MM'] en son milieu

Autrement dit, M et M' sont symétriques par rapport à une droite (d) si (d) est la médiatrice du segment [MM'].

Remarque: Transformer une figure par une symétrie axiale, c'est créer l'image de cette figure par pliage le long de l'axe.

Construction:

Construction de la symétrie d'un rectangle par une symétrie axiale (avec l'équerre):

Construction de la symétrie d'un rectangle par rapport à une droite (avec le compas)

Construction d'images de figures:

Propriétés de la symétrie axiale:

2. Symétrie centrale:

Deux points M et M' sont symétrique par rapport à un point O si O est le milieu du segment [MM'].

Remarque:

Transformer une figure par une symétrie centrale, c'est créer l'image de cette figure par

un demi-tour autour du centre.

Construction:

Symétrie d'une figure par une symétrie centrale (avec des carreaux ou du papier pointé):

Image d'une figure par une symétrie centrale (sans carreaux):

Utiliser les propriétés des symétries (axiale et centrale):

3) Translation:

Le point M' est l'image d'un point M par la translation qui transforme un point A en un point B si le quadrilatère MM'BA est un parallélogramme.

Remarque:

Transformer une figure par une translation, c'est créer l'image de cette figure par rapport à un glissement d'un point à un autre point.

Construction:

Image d'une figure par une translation (avec des carreaux):

Image d'une figure par une translation en utilisant l'équerre, la règle et le compas:

Image d'un point par une translation (sans carreaux) avec le compas:

4) Rotation:

Le point M' est l'image d'un point M par la rotation de centre O d'angle a° dans le sens inverse dans aiguilles d'une montre ou anti-horaire (ou positif ou direct) si:

• OM = OM'.

• l'angle MOM' = a° (dans le sens inverse des aiguilles d'une montre)

Remarque:

Transformer une figure par rotation, c'est créer l'image de cette figure par une rotation autour du centre suivant un angle donné et dans un sens donné.

Construction:

Image d'une figure avec un quadrillage (avec des carreaux):

Image d'un point par une rotation:

Image d'un triangle par une rotation:

Remarque:

Une rotation de centre 0, d'angle 180° et quel que soit le sens est une symétrie de centre O.

II. Homothétie:

1. Homothétie de rapport positif:

M' est l'image d'un point M par l'homothétie de centre O et de rapport k (k>0) signifie que:

• O, M, M' sont alignés.

• M et M' sont du même coté par rapport à O, donc M appartient à [OM'] ou M' appartient à [OM].

• OM' = k OM.

Ici k = 2 :

Exemples:

Remarque:

Si k>1, alors l'homothétie correspond à un agrandissement.

Si 0<k<1, alors l'homothétie correspond à une réduction.

Définition:

Homothéties de rapport positif (avec des carreaux):

Vidéos à venir... Juin 2024...

2) Homothétie de rapport négatif.

M' est l'image d'un point M par l'homothétie de centre O et de rapport k (k<0) signifie que:

• O, M, M' sont alignés.

• M et M' ne sont pas du même coté par rapport à O, donc O appartient à [MM']

• OM' = (-k) OM.

ici, k = -0,5:

Exemples:

Image d'un point par une homothétie:

Image d'une figure par une homothétie (sans compas mais en calculant les longueurs):

Image d'une figure par une homothétie (avec le compas):

Effet de l'homothéties sur les longueurs et les aires:

Pour s'entraîner (avec corrigé):

Effet d'agrandissements ou de réductions sur les aires: